第二章 递归与分治策略（一）

2.1 递归

直接或间接地调用自身的算法称为递归算法。

用函数自身给出定义的函数称为递归函数。

2.1.1 阶乘函数

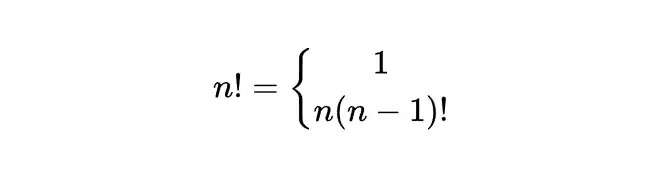
n(n-1)!调用自身，将主问题拆分成若干层的子问题。

#include<bits/stdc++.h>
using namespace std;
int jiecheng(int n){
    if(n==0)
        return 1;
    else
        return n*jiecheng(n-1);
}
int main(){
    int n;
    cin>>n;
    cout<<jiecheng(n);
    return 0;
}

先分解再解决的过程，先把问题分解到足够小，再从小问题开始逐一向上击破。

2.1.2 斐波那契数列

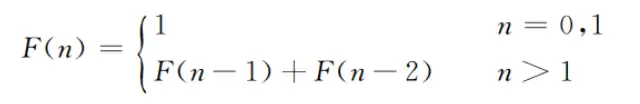
#include<bits/stdc++.h>
using namespace std;
fb(int n){
    if(n==1||n==2) return 1;
    return fb(n-1)+fb(n-2);
}
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cout<<fb(i)<<endl;
    }
    return 0;
}

2.1.3 Ackerman函数

双递归函数

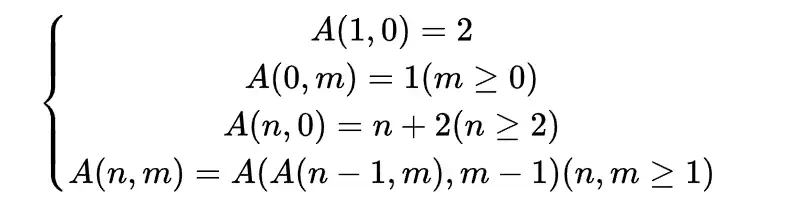
2.1.4 汉诺塔问题

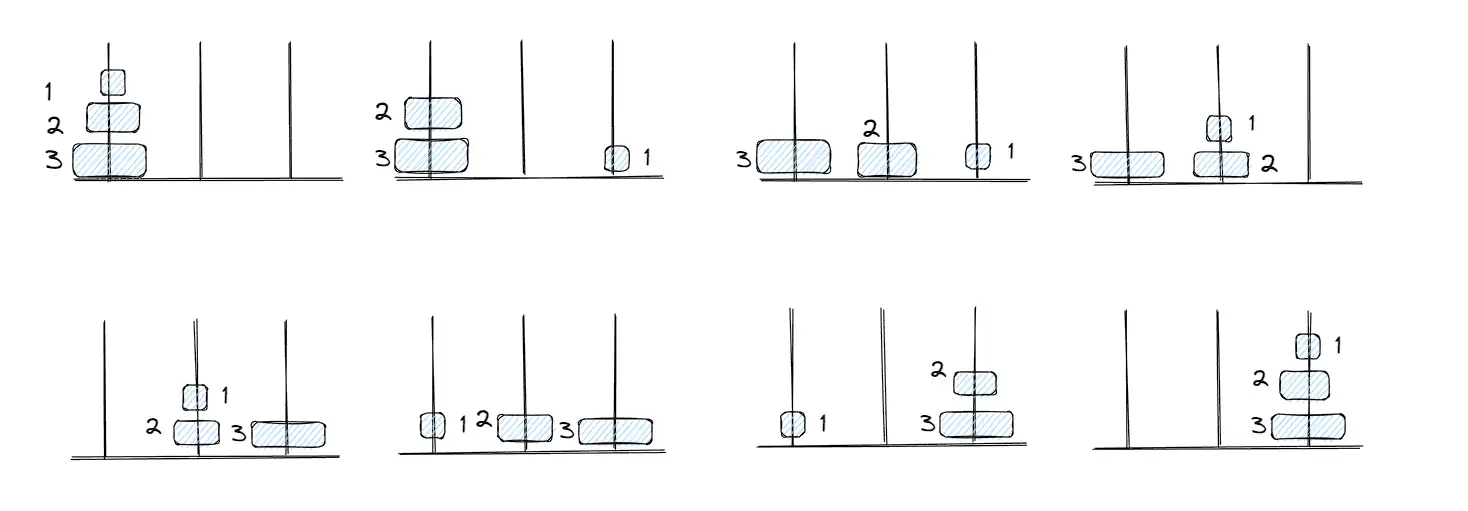
设a,b,c是3个塔座。开始时，在塔座a上有一叠共n个圆盘，这些圆盘自下而上，由大到小地叠在一起。各圆盘从小到大编号为1，2，...,n，现要求将塔座a上的这一叠圆盘移到塔座c上，并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则：

规则1：每次只能移动1个圆盘；

规则2：任何时刻都不允许将较大的圆盘压在较小的圆盘之上；

规则3：在满足规则1和2的前提下，可将圆盘移至a,b,c中任一塔座上。

eg.三层

临界条件：只需要移动一个盘子时，直接把盘子从 a 移动到 c ；
递归函数：每次将 a 柱上除了最底下的所有盘子借助 c 移到 b，再把 a 柱最底下的盘子移到 c，最后将 b 柱上的盘子全部移到 c ，每次的整体移动都需要递归应用自身，两次递归运用中移动的盘子数相等，只是比上一层小一。

#include<bits/stdc++.h>
using namespace std;
void move(char a,char b){
    cout<<a<<"->"<<b<<endl;
}
void hanoi(int n,char a,char b,char c){
    if(n==1) move(a,c);
    else{
        hanoi(n-1,a,c,b);
        move(a,c);
        hanoi(n-1,b,a,c);
    }
}
int main(){
    int n;
    char a,b,c;
    cin>>n>>a>>b>>c;
    hanoi(n,a,b,c);
    return 0;
}

2.2 分治

2.2.1 原理

将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

其中的划分再击破，和递归的分解再解决异曲同工，其实同样用到了递归的思想，只不过分治法先分再治，最后还得合并。

设计模板：

divide_and_conquer ( P ) {  
    if ( P <= n0 ) return conquer ( P ) ; 当P的规模不超过阈值n0时，直接求解。
    divide P into P1, P2, P3 ... Pk ;           分解问题P为各个子问题
    for ( i = 1 ; i <= k ; i++ )                 
            yi = divide_and_conquer ( Pi ) ;   递归求解子问题
    return merge ( y1, y2, y3 ... yk ) ;         合并子问题的解为P的解
}

2.1.2 分治法时间复杂度

一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。为方便起见，设分解阈值no=1，且conquer解规模为1的问题耗费1个单位时间。

另外，再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f（n)个单位时间。如果用T(n)表示该分治法divide-and-conquer（P）解规模为 P=n 的问题所需的计算时间，则有

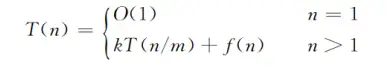
展开递归式，反复待入求解

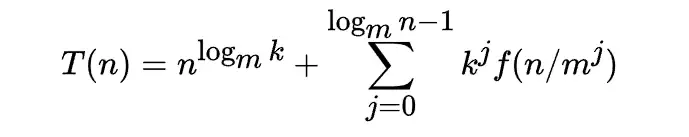
通常可以假定T(n)单调上升。

2.3 二分搜索技术

要求：给定已按升序拍好序的 n 个元素，需要在这 n 个元素中找出一个特定元素 x 。

分析：逐一对比来搜索的话，时间复杂度为O(n)，但是使用二分搜索，每次折半查找，时间复杂度仅为O(log n)，理论存在，实践开始！

思路：使用递归的思想，临界条件是最后找不到目标元素，递归函数就是每次折半，若折半后取到目标元素，就直接返回，如果折半取到的元素大于目标元素，就搜索前半部分，否则搜索后半部分。

代码：递归和循环，时间复杂度都为O(log n)

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6;
int n,x,a[N];
int bisearch (int x, int a[], int left, int right) {
    if (left > right) return -1;
    int middle = left + right >> 1;
    if (a[middle] == x) 
        return middle;
    else if (a[middle] > x)
        return bisearch (x, a, left, middle-1);
    else
        return bisearch (x, a, middle+1, right);
}
int main() {
    cin >> n;
    for (int i = 0; i < n; i++)
        cin  >> a[i];
    cin  >> x;
    cout << bisearch (x, a, 0, n-1);
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6;
int n, x, a[N];
int bisearch (int x, int a[], int left, int right) {
    while(left <= right) {
        int middle = left + right >> 1;
        if (a[middle] == x)
            return middle;
        else if (a[middle] > x)
            return bisearch (x, a, left, middle-1);
        else
            return bisearch (x, a, middle+1, right);
    }
    return -1;
}
int main () {
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> a[i];
    cin >> x;
    cout << bisearch (x, a, 0, n-1);
    return 0;
}

最坏情况下O(log n)